## 二叉查找树
  1. 若它的左子树不为空，则左子树上所有的节点值都小于它的根节点值。
  2. 若它的右子树不为空，则右子树上所有的节点值均大于它的根节点值。
  3. 它的左右子树也分别可以充当为二叉查找树。
img
img

缺点：大部分节点都倾向一边的情况下时间复杂度几乎是线性的

平衡二叉树

  1. 具有二叉查找树的全部特性。
  2. 每个节点的左子树和右子树的高度差至多等于1。

右旋

我们在进行节点插入的时候，可能会出现节点都倾向于左边的情况，例如：

img
img

我们把这种倾向于左边的情况称之为 左-左型。这个时候，我们就可以对节点9进行右旋操作，使它恢复平衡。

img

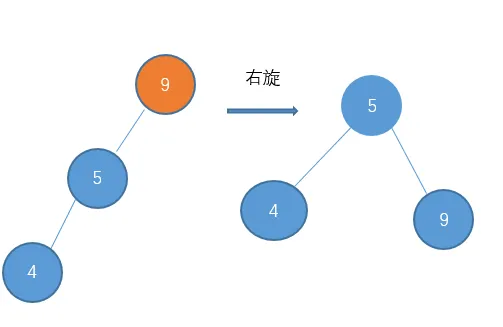
即：顺时针旋转两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子

再举个例子：

img

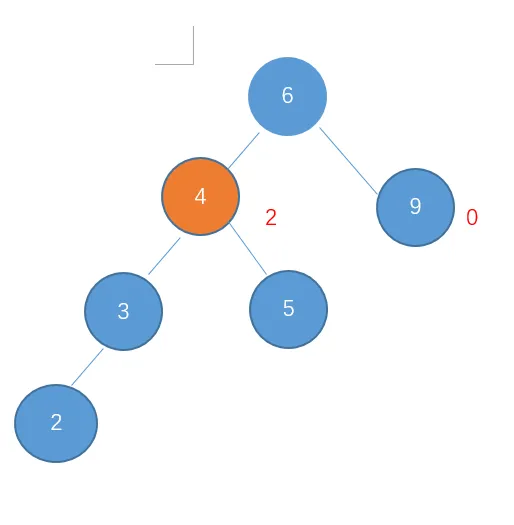
节点4和9高度相差大于1。由于是左孩子的高度较高，此时是左-左型，进行右旋。

img
img

这里要注意，节点4的右孩子成为了节点6的左孩子了

左旋

左旋和右旋一样，就是用来解决当大部分节点都偏向右边的时候，通过左旋来还原。例如：

img

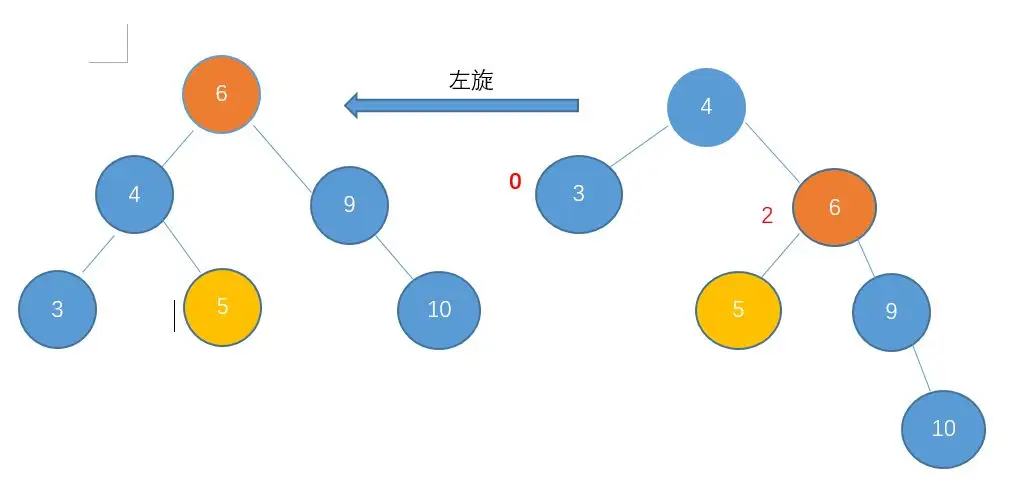
我们把这种倾向于右边的情况称之为 右-右型。

注意：5 成为了 4 的右孩子

右-左旋

img
img

出现了这种情况怎么办呢?对于这种 右-左型 的情况，单单一次左旋或右旋是不行的。

img
img

这种我们就把它称之为 右-左 型吧。处理的方法是先对节点10进行右旋把它变成右-右型。

img
img

然后再进行左旋。

img
img

所以对于这种 右-左型的，我们需要进行一次右旋再左旋。

同理，也存在 左-右型的，例如：

img
img

对于左-右型的情况和刚才的 右-左型相反，我们需要对它进行一次左旋，再右旋。

img
img

到此，我们的插入就结束了。

总结

在插入的过程中，会出现一下四种情况破坏AVL树的特性，我们可以采取如下相应的旋转。

1、左-左型：做右旋。

2、右-右型：做左旋。

3、左-右型：先做左旋，后做右旋。

4、右-左型：先做右旋，再做左旋。

左右旋感觉怪怪的？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
//定义节点
class AvlNode {
   int data;
   AvlNode lchild;//左孩子
   AvlNode rchild;//右孩子
   int height;//记录节点的高度
}

//在这里定义各种操作
public class AVLTree{
   //计算节点的高度
   static int height(AvlNode T) {
       if (T == null) {
           return -1;
       }else{
           return T.height;
       }
   }

   //左左型，右旋操作
   static AvlNode R_Rotate(AvlNode K2) {
       AvlNode K1;

       //进行旋转
       K1 = K2.lchild;
       K2.lchild = K1.rchild;
       K1.rchild = K2;

       //重新计算节点的高度
       K2.height = Math.max(height(K2.lchild), height(K2.rchild)) + 1;
       K1.height = Math.max(height(K1.lchild), height(K1.rchild)) + 1;

       return K1;
   }

   //右右型，进行左旋
   static AvlNode L_Rotate(AvlNode K2) {
       AvlNode K1;

       K1 = K2.rchild;
       K2.rchild = K1.lchild;
       K1.lchild = K2;

       //重新计算高度
       K2.height = Math.max(height(K2.lchild), height(K2.rchild)) + 1;
       K1.height = Math.max(height(K1.lchild), height(K1.rchild)) + 1;

       return K1;
   }

   //左-右型，进行右旋，再左旋
   static AvlNode R_L_Rotate(AvlNode K3) {
       //先对其孩子进行右旋
       K3.lchild = R_Rotate(K3.lchild);
       //再进行左旋
       return L_Rotate(K3);
   }

   //右-左型，先进行左旋，再右旋
   static AvlNode L_R_Rotate(AvlNode K3) {
       //先对孩子进行左旋
       K3.rchild = L_Rotate(K3.rchild);
       //再右旋
       return R_Rotate(K3);
   }

   //插入数值操作
   static AvlNode insert(int data, AvlNode T) {
       if (T == null) {
           T = new AvlNode();
           T.data = data;
           T.lchild = T.rchild = null;
       } else if(data < T.data) {
           //向左孩子递归插入
           T.lchild = insert(data, T.lchild);
           //进行调整操作
           //如果左孩子的高度比右孩子大2
           if (height(T.lchild) - height(T.rchild) == 2) {
               //左-左型
               if (data < T.lchild.data) {
                   T = R_Rotate(T);
               } else {
                   //左-右型
                   T = R_L_Rotate(T);
               }
           }
       } else if (data > T.data) {
           T.rchild = insert(data, T.rchild);
           //进行调整
           //右孩子比左孩子高度大2
           if(height(T.rchild) - height(T.lchild) == 2)
               //右-右型
               if (data > T.rchild.data) {
                   T = L_Rotate(T);
               } else {
                   T = L_R_Rotate(T);
               }
       }
       //否则，这个节点已经在书上存在了，我们什么也不做
       
       //重新计算T的高度
       T.height = Math.max(height(T.lchild), height(T.rchild)) + 1;
       return T;
   }
}

参考：https://mp.weixin.qq.com/s/dYP5-fM22BgM3viWg4V44A